Spatio-temporal Analysis of event-related fMRI data¶
In this example we are going to take a look at an event-related analysis of timeseries data. We will do this on fMRI data, implementing a spatio-temporal analysis of multi-volume samples. It starts as usual by loading PyMVPA and the fMRI dataset.
from mvpa2.suite import *
ds = load_tutorial_data(roi=(36,38,39,40))
The dataset we have just loaded is the full timeseries of voxels in the ventral temporal cortex for 12 concatenated experiment runs. Although originally a block-design experiment, we’ll analyze it in an event-related fashion, where each stimulation block will be considered as an individual event.
For an event-related analysis most of the processing is done on data samples that are somehow derived from a set of events. The rest of the data could be considered irrelevant. However, some preprocessing is only meaningful when performed on the full timeseries and not on the segmented event samples. An example is the detrending that typically needs to be done on the original, continuous timeseries.
In its current shape our dataset consists of 1452 samples that represent
contiguous fMRI volumes. At this stage we can easily perform linear
detrending. We are going to do it per each experiment run (the dataset has
to have runs encoded in the chunk sample attribute), since we do not assume a
contiguous linear trend throughout the whole recording session.
# detrend on full timeseries
poly_detrend(ds, polyord=1, chunks_attr='chunks')
Let’s make a copy of the detrended dataset that we can later on use for some visualization.
orig_ds = ds.copy()
We still need to normalize each feature (i.e. a voxel at this point). In this case we are going to Z-score them, using the mean and standard deviation from the experiment’s rest condition. The resulting values might be interpreted as “activation scores”. We are again doing it per each run.
zscore(ds, chunks_attr='chunks', param_est=('targets', 'rest'))
After detrending and normalization, we can now segment the timeseries into a set of events. To achieve this we have to compile a list of event definitions first. In this example we will simply convert the block-design setup defined by the samples attributes into events, so that each stimulation block becomes an event with an associated onset and duration. The events are defined by a change in any of the provided attributes, hence we get an event for starting stimulation block and any start of a run in the experiment.
events = find_events(targets=ds.sa.targets, chunks=ds.sa.chunks)
events is a simple list of event definitions (each one being a
dictionary) that can easily inspected for startpoints and duration of
events. Later on we want to look at the sensitivity profile ranging from
just before until a little after each block. Therefore we are slightly
moving the event onsets prior the block start and request to extract a
set of 13 consecutive volumes a as sample for each event. Finally, in this
example we are only interested in face or house blocks.
# filter out events
events = [ev for ev in events if ev['targets'] in ['house', 'face']]
# modify event start and set uniform duration
for ev in events:
ev['onset'] -= 2
ev['duration'] = 13
Now we get to the core of an event-related analysis. We turn our existing timeseries datasets into one with samples of timeseries segments.
PyMVPA offers eventrelated_dataset()
to perform this conversion – given a list of events and a dataset with
samples that are sorted by time. If a dataset has information about
acquisition time eventrelated_dataset()
can also convert event-definition in real time.
evds = eventrelated_dataset(ds, events=events)
Now we have our final dataset with spatio-temporal fMRI samples. Look at the attributes of the dataset to see what information is available about each event. The rest is pretty much standard.
We want to perform a cross-validation analysis of a SVM classifier. We are not primarily interested in its performance, but in the weights it assigns to the features. Remember, each feature is now voxel-timepoint, so we get a chance of looking at the spatio-temporal profile of classification relevant information in the data. We will nevertheless enable computing a confusion matrix, so we can assure ourselves that the classifier is performing reasonably well, since only a generalizing classifier model is worth inspecting, as otherwise the assigned weights are meaningless.
clf = LinearCSVMC()
sclf = SplitClassifier(clf, enable_ca=['stats'])
# Compute sensitivity, which internally trains the classifier
analyzer = sclf.get_sensitivity_analyzer()
sensitivities = analyzer(evds)
Now let’s look at the confusion matrix – it turns out that the classifier performs excellent.
print sclf.ca.stats
We could now convert the computed sensitivities back into a 4D fMRI image to look at the spatio-temporal sensitivity profile using the datasets mapper. However, in this example we are going to plot it for two example voxels and compare it to the actual signal timecourse prior and after normalization.
# example voxel coordinates
example_voxels = [(28,25,25), (28,23,25)]
First we plot the orginal signal after initial detrending. To do this, we apply the timeseries segmentation to the original detrended dataset and plot to mean signal for all face and house events for both of our example voxels.
vx_lty = ['-', '--']
t_col = ['b', 'r']
pl.subplot(311)
for i, v in enumerate(example_voxels):
slicer = np.array([tuple(idx) == v for idx in ds.fa.voxel_indices])
evds_detrend = eventrelated_dataset(orig_ds[:, slicer], events=events)
for j, t in enumerate(evds.uniquetargets):
pl.plot(np.mean(evds_detrend[evds_detrend.sa.targets == t], axis=0),
t_col[j] + vx_lty[i],
label='Voxel %i: %s' % (i, t))
pl.ylabel('Detrended signal')
pl.axhline(linestyle='--', color='0.6')
pl.legend()
In the next step we do exactly the same again, but this time for the normalized data.
pl.subplot(312)
for i, v in enumerate(example_voxels):
slicer = np.array([tuple(idx) == v for idx in ds.fa.voxel_indices])
evds_norm = eventrelated_dataset(ds[:, slicer], events=events)
for j, t in enumerate(evds.uniquetargets):
pl.plot(np.mean(evds_norm[evds_norm.sa.targets == t], axis=0),
t_col[j] + vx_lty[i])
pl.ylabel('Normalized signal')
pl.axhline(linestyle='--', color='0.6')
Finally, we plot the associated SVM weight profile for each peristimulus
timepoint of both voxels. For easier selection we do a little trick and
reverse-map the sensitivity profile through the last mapper in the
dataset’s chain mapper (look at evds.a.mapper for the whole chain).
This will reshape the sensitivities into cross-validation fold x volume x
voxel features.
pl.subplot(313)
smaps = evds.a.mapper[-1].reverse(sensitivities)
for i, v in enumerate(example_voxels):
slicer = np.array([tuple(idx) == v for idx in ds.fa.voxel_indices])
smap = smaps.samples[:,:,slicer].squeeze()
plot_err_line(smap, fmt='ko', linestyle=vx_lty[i])
pl.xlim((0,12))
pl.ylabel('Sensitivity')
pl.axhline(linestyle='--', color='0.6')
pl.xlabel('Peristimulus volumes')
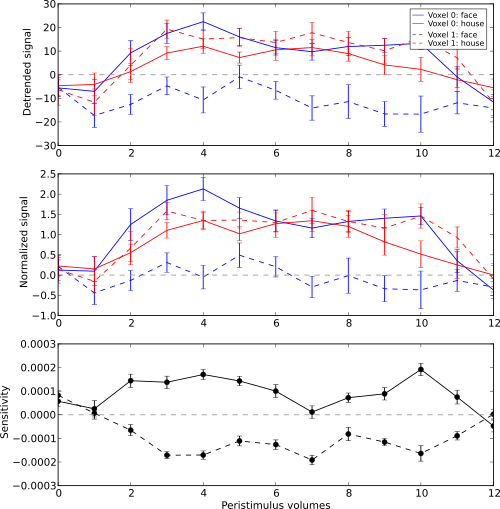
Sensitivity profile for two example voxels for face vs. house classification on event-related fMRI data from ventral temporal cortex.
This demo showed an event-related data analysis. Although we have performed it on fMRI data, an analogous analysis can be done for any timeseries-based data in an almost identical fashion.
See also
The full source code of this example is included in the PyMVPA source distribution (doc/examples/eventrelated.py).




